Splątanie kwantowe z poziomu nanosatelity. Nowy rozdział badań

Najnowszy eksperyment orbitalny ze splątanymi stanami kwantowymi fotonów przeprowadzono z wykorzystaniem miniaturowego satelity typu CubeSat (w standardzie tym, 1U odpowiada sześciennej konstrukcji o długości krawędzi równej 10 cm), SpooQy-1. Nanosatelita zbudowany został z trzech jednostek (3U), przy czym systemy sterowania, łączności i zasilania zamknięto w jednej (1U). Pozostałe dwa bloki zajęło oprzyrządowanie samego eksperymentu kwantowego.

Misja została przeprowadzona przez Centrum Technologii Kwantowych w Singapurze, we współpracy z partnerami ze Szwajcarii, Australii i Wielkiej Brytanii. SpooQy-1 powstał na bazie wcześniejszego projektu nanosatelitarnego Galassia (2U), który w 2016 roku wykonał orbitalne testy układu do generowania splątanych stanów kwantowych [1]. W ramach tej misji nie udało się jednak dokonać pomiarów samego splątania kwantowego.

Z uwagi na stosunkowo niskie koszty zarówno budowy, jak i umieszczania na niskiej orbicie okołoziemskiej CubeSatów, przeprowadzona misja toruje drogę do powszechniejszej realizacji satelitarnych projektów kwantowych. Ich prowadzenie i dalsze rozwijanie pojawia się w zasięgu coraz mniejszych grup naukowców i inżynierów z różnych ośrodków oraz części świata.

Fizyka u podstaw technologicznego przeskoku

Żeby odpowiednio unaocznić znaczenie eksperymentu przeprowadzonego na pokładzie nanosatelity SpooQy-1, warto przypomnieć najpierw, co rozumiemy przez splątanie kwantowe. Fotony – jako podstawowe porcje (kwanty) pola elektromagnetycznego – oprócz odpowiadającej im długości fali, czy też zbioru długości fali składających się na tak zwaną paczkę falową, posiadają również dwa wewnętrzne stopnie swobody związane z ich polaryzacją. Wypadkowa polaryzacja fotonu ma postać kwantowej superpozycji dwóch stanów bazowych polaryzacji. Jako stany bazowe możemy wybrać przykładowo dwie prostopadłe względem siebie polaryzacje: poziomą (H – horizontal) oraz pionową (V – vertical). Kierunki polaryzacji są ustalone względem referencyjnego układu odniesienia – takiego, jaki wyznacza chociażby płaszczyzna stołu optycznego.

Fotony możemy przygotować w stanach o pożądanej polaryzacji liniowej, przepuszczając je przez polaryzator. Jeśli będzie on ustawiony np. w pozycji H, to foton o początkowej dowolnej polaryzacji, po przejściu przez taki polaryzator znajdzie się stanie H. Ciekawą sytuacją jest, kiedy pozycja polaryzatora nie będzie pokrywała się z jedną z pozycji bazowych H i V, lecz np. będzie względem każdej z nich obrócona o 45 stopni - odpowiada to wówczas polaryzacji diagonalnej (D – diagonal) oraz antydiagonalnej (A – anti-diagonal).

Wtedy to, analizując np. foton w stanie o polaryzacji D za pomocą analizatora złożonego z polaryzatorów ustawionych w pozycjach H i V, zaobserwujemy tak zwaną redukcji stanu kwantowego. Statystycznie, przepuszczając przez analizator pewną liczną fotonów przygotowanych w stanie D, połowę z nich zarejestrujemy jako będące w stanie H, a połowę w stanie V. Stan o polaryzacji D możemy więc uznać za superpozycję kwantową stanów bazowych H i V, z jednakowym rozkładem prawdopodobieństw równym 1/2. W trakcie aktu pomiaru, jakim jest analiza polaryzacji, stan ten redukuje się do jednego ze stanów bazowych (H,V) i pozostaje w nim.

Mówiąc o koncepcji superpozycji kwantowej w kontekście splątania kwantowego, punktem odniesienia dla dalszych rozważań są stany kwantowe dwóch fotonów. Takie też stany wygenerowane zostały w ramach misji SpooQy-1. Jest to zresztą sytuacja najpowszechniejsza, gdyż wytwarzanie stanów splątanych trzech i większej liczby fotonów to wciąż raczkujący obszar doświadczalnej optyki kwantowej.

Zjawisko splątania kwantowego jest szczególnym typem superpozycji w układzie cząstek, prowadzące do występowania nielokalnych korelacji pomiędzy nimi. Stanami dwufotonowymi, w których możemy zaobserwować splątanie, są w szczególności stany Bella: Φ+, Φ-, Ψ+ i Ψ-. Stany te są szczególnie interesujące, gdyż należą do przypadku, w którym splątanie kwantowe jest najsilniejsze (mówimy, że są to stany maksymalnie splątane).

Przyjrzyjmy się bliższej przypadkowi fotonów w stanie Φ+. Fotony takie, wyemitowane ze źródła stanu splątanego, propagują się następnie do odległych punktów A i B, w których następuje pomiar. Podobnie, jak w omawianym powyżej przypadku pojedynczego fotonu, odgórnie możemy z równym prawdopodobieństwem oczekiwać zarejestrowania każdego z fotonów w stanie o jednej z dwóch polaryzacji: H lub V.

W tym momencie dochodzimy jednak do jednej z najbardziej enigmatycznych własności mechaniki kwantowej. Mianowicie, jeśli dokonamy analizy polaryzacji jednego z fotonów, to będzie to miało natychmiastowy wpływ na wynik pomiaru przeprowadzonego na tym drugim. Jeśli np. w wyniku pomiaru okaże się, że foton w punkcie A jest stanie o polaryzacji H, to ze stuprocentową pewnością, analizując drugi foton w punkcie B, zaobserwujemy, że znajduje się on również w stanie H. Natomiast, jeśli nie dokonalibyśmy pomiaru w punkcie A, to wynik pomiaru w punkcie B wynosiłby w 50% przypadków H i w 50% przypadków V.

Ta natychmiastowa redukcja stanu kwantowego, odbiegająca od tak zwanego lokalnego realizmu, okazała się trudna do zaakceptowania przez wielu fizyków, co znalazło ucieleśnienie między innymi w paradoksie EPR (Einsteina-Podolskiego-Rosena). Przypuszczano, że mogą istnieć pewne dodatkowe (nieobserwowane) stopnie swobody, tak zwane zmienne ukryte, o których wiedza pozwoliłaby przewidzieć wyniki pomiarów i uniknąć konieczności natychmiastowej redukcji stanu kwantowego pomiędzy odległymi punktami. Możliwość występowania zmiennych ukrytych, przynajmniej tych lokalnego typu, wyeliminował ostatecznie w latach sześćdziesiątych ubiegłego wieku północnoirlandzki fizyk John Bell – ten sam, od którego nazwiska pochodzi wprowadzona powyżej rodzina stanów kwantowych.

Rozważając korelacje pomiędzy wynikami pomiarów w punktach A, B wykazał on, że hipoteza zmiennych ukrytych wymaga spełnienia określonej nierówności pomiędzy wynikami pomiarów w różnych bazach. Jak postulował Bell, teoria lokalnych zmiennych ukrytych wymaga, żeby wielkość zwana parametrem CHSH (Clauser-Horne-Shimony-Holt) – pod postacią: S = E(a,b) – E(a,b’) + E(a’,b) + E(a’,b’) – spełniała następującą nierówność (zwana nierównością Bella, lub też nierównością Bella-CHSH): |S|≤ 2.

Zainteresowani szerszym wyjaśnieniem powyższego wątku teoretycznego mogą zapoznać się z nim w poszerzonej wersji artykułu - zamieszczonego na autorskim blogu.

Okazuje się jednak, że stany splątane, takie jak rozważane tu stany Bella, jawnie łamią tę nierówność, przecząc lokalnemu realizmowi. Wynik ten wspiera postrzeganie mechanik kwantowej jako teorii w pewnym stopniu nielokalnej. Mianowicie, stan splątany dwóch cząstek kwantowych traktujemy jako jeden obiekt kwantowy i niezależnie od tego, czy jedna jego część znajduje się w dużej odległości od drugiej, ingerencja w tą pierwszą poniesie za sobą natychmiastowy skutek dla tej drugiej i vice versa.

Wbrew pierwotnym obawom, wyrażonym w paradoksie EPR, nie jest w ten sposób możliwa nadświetlna wymiana informacji. Pomimo, że splątanie kwantowe nie pozwala urzeczywistnić wizji znanych chociażby z sagi Star Trek, umożliwia zastosowanie w komunikacji – za sprawą zarówno możliwości przeprowadzania za jej pośrednictwem tak zwanej teleportacji stanów kwantowych, jak i kwantowej dystrybucji klucza. Oba te procesy zachodzą z prędkością światła w danym ośrodku, która jest mniejsza lub równa prędkości światła w próżni.

Nie takie znowu „upiorne oddziaływanie na odległość”… czyli splątanie w praktyce

Kwantowa dystrybucja klucza, czyli drugie ze wskazanych zastosowań praktycznych zjawiska splątania kwantowego, stanowi jeden z filarów kryptografii kwantowej. Przyciąga szczególnie duże zainteresowanie inżynieryjno-badawcze i stanowi jedną z głównych motywacji do przeprowadzenia misji takich jak SpooQy-1. Wytworzone w takich przypadkach stany Bella pozwalają m.in. na zastosowanie protokołu Ekerta (E91) kwantowej dystrybucji klucza [2].

W podejściu tym, zaufana jednostka (na przykład nanosatelita) wytwarza pary splątanych fotonów, wysyłając jeden z nich do punku A, a drugi do punktu B. Analizując otrzymane fotony, można otrzymać ciągi wyników pomiaru polaryzacji, np. HVHHVHVHV…. Przypisując zaś stanom polaryzacji wartości binarne np. H->0 i V->1, otrzymujemy ciąg bitów 010010101…, który może stanowić sekretny klucz, stosowany w protokołach klasycznej kryptografii symetrycznej.

Przygotowując fotony np. w stanie Φ+, mamy pewność, że jeśli odbiorca A zarejestrował ciąg 010010101…, to taki sam ciąg zaobserwuje również odbiorca klucza w punkcie B. Dodatkowym elementem takiego protokołu jest sprawdzenie na części odbieranych bitów tego, czy nie nastąpił podsłuch transmisji. Po pomyślnej weryfikacji, uzyskujemy wynikającą z praw mechaniki kwantowej gwarancję poufności wymienionego klucza.

Za pomocą satelity SpooQy-1 przeprowadzono testy zarówno wytwarzania, jak i analizy stanów splątanych. Splątane fotony nie były jednak emitowane poza nanosatelitę, do odbiorców w przestrzeni kosmicznej lub na powierzchni Ziemi. To już będzie stanowiło przedmiot kolejnych misji. W ramach tego projektu, cały eksperyment został przeprowadzony w obrębie zamkniętego modułu doświadczalnego, zawierającego źródło splatanych fotonów oraz ich analizator.

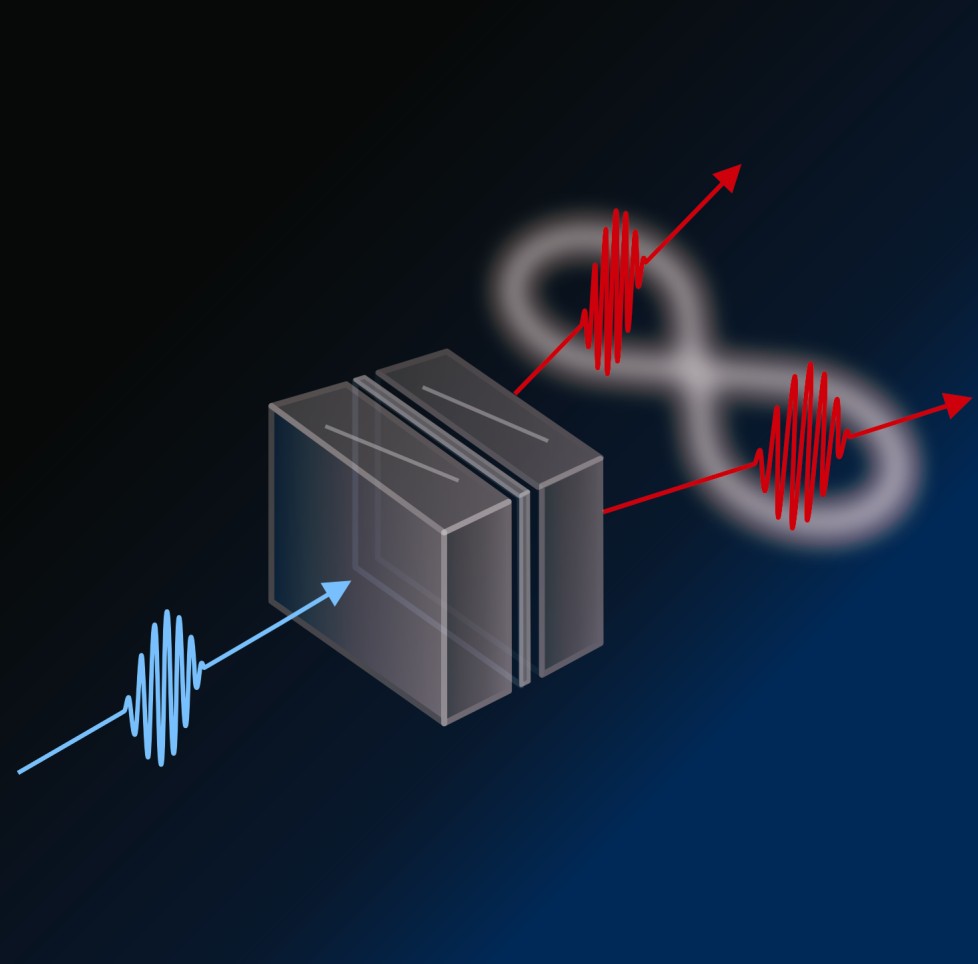
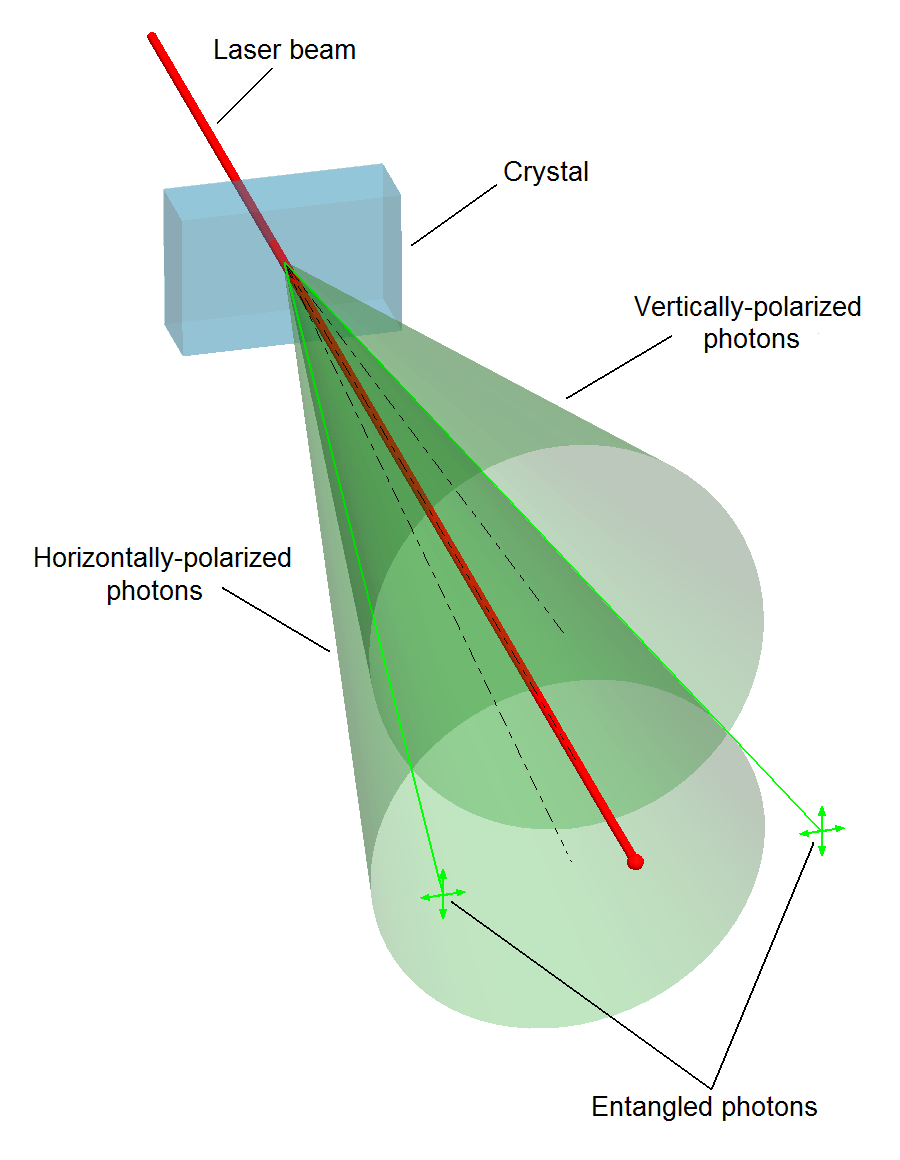
Do wytworzenia par splątanych kwantowo fotonów wykorzystano, powszechnie stosowany w warunkach laboratoryjnych, proces zwany spontanicznym parametrycznym obniżaniem częstości (SPDC – Spontaneous Parametric Down-Conversion). W zjawisku tym, wysokoenergetyczny (np. ultrafioletowy) foton ulega w optycznie nieliniowym ośrodku konwersji na dwa niżej-energetyczne fotony, występujące już w stanie splątanym. Wyniki przeprowadzonego eksperymentu raportują o wytworzeniu w ten sposób, w warunkach kosmicznych, stanu Bella Φ- (jest to stan bardzo podobny do stanu Φ+, różniący się od niego jedynie względną fazą pomiędzy stanami bazowymi).

W układzie eksperymentalnym jako źródło fotonów zastosowano diodę laserową (LD), generującą wiązkę fotonów o długości fali 405 nm (granica światła widzialnego, w stronę bliskiego ultrafioletu) i szerokości spektralnej równej 160 MHz. Do wytworzenia stanów splątanych wykorzystano dwie płytki wykonane z boranu baru (BBO), pomiędzy którymi ustawiono płytkę półfalową (HWP), dokonującą obrotu polaryzacji o 90 stopni.

W celu usunięcia z wiązki wejściowego (pompującego) światła laserowego, które nie uległo konwersji w procesie SPDC, zastosowano lustro dichroiczne (DM1), pełniące funkcję filtru. Natomiast, aby skompensować dyspersję otrzymanych fotonów na drodze optycznej zastosowano kryształ wanadanu (V) itru – YVO4. Tak otrzymany sygnał został rozdzielony do dwóch analizatorów za pomocą kolejnego lustra dichroicznego (DM2). Każdy z nich składał się z ciekłokrystalicznego rotatora polaryzacji (LCPR), polaryzatora (P) oraz fotodiody lawinowej (GM-APD) i analizował jeden z fotonów należący do kwantowo splątanej pary. Zarejestrowane fotony uznawano za pochodzące z jednej splątanej kwantowo pary, jeśli zaobserwowano je w oknie czasowym o rozpiętości ~ 5 ns.

Doniosłe wnioski z misji niepozornego satelity

Za pomocą takiego układu doświadczalnego, przeprowadzono eksperyment, w którym wykazano, że wartość parametru S, dla wytworzonych w procesie SPDC stanów Bella przyjmuje wartości większe od klasycznej granicy S=2, a mniejsze od teoretycznie przewidzianej wartości równej S=2√2≈2.83. Uśredniona, otrzymana w ramach eksperymentu wartość to S=2.60±0.07 > 2. Potwierdzono tym samym łamanie nierówności Bella w warunkach orbitalnych.

Otrzymany w eksperymencie poziom błędów, odpowiadający parametrowi QBER (Quantum Bit Error Rate) równemu ~ 4 procent (około cztery na 100 transmitowanych bitów są błędne), jest wystarczający do tego, żeby pomyślnie przeprowadzać kwantową dystrybucję klucza. To wymagać będzie jednak dostosowania układu doświadczalnego do pracy z laserem o większej mocy i układem optycznym umożliwiającym dalekodystansową komunikację optyczną.

Przybliżone tu wyniki grupy z Centrum Technologii Kwantowych w Singapurze, którego dyrektorem do niedawna pozostawał Polak prof. Artur Ekert, to z jednej strony zwieńczenie wielu lat intensywnej pracy, a z drugiej preludium do kolejnych, jeszcze szerzej zakrojonych, kwantowych projektów kosmicznych. Do następnych milowych kroków należą niewątpliwie: przeprowadzanie kwantowej dystrybucji klucza pomiędzy dwoma nanosatelitami [3] oraz pomiędzy nanosatelitą a stacją naziemną [4].

Prace w tym kierunku, w szczególności w kontekście wykorzystania łatwiejszej wersji kwantowej dystrybucji klucza, nie opartej na splątaniu kwantowym, już trwają. Ponadto, nanosatelitarne eksperymenty ze splątaniem kwantowym w warunkach orbitalnych otwierają możliwość do badań podstawowych, szczególnie w kontekście związku pomiędzy teorią grawitacji a fizyką kwantową.

Warte podkreślenia jest to, że dzięki wykorzystaniu platform typu CubeSat, projekty tego typu stają się możliwie do realizacji również w warunkach polskich. W kierunku tym zwracamy się ramach działającego na Uniwersytecie Jagiellońskim w Krakowie zespołu naukowego Quantum Cosmos Lab.

Przypisy:

[1] Zhongkan Tang, et al., Generation and Analysis of Correlated Pairs of Photons aboard a Nanosatellite, Phys. Rev. Applied 5, 054022  (2016).
[2] Artur K. Ekert, Quantum cryptography based on Bell’s theorem, Phys. Rev. Lett. 67, 661 (1991).
[3] Denis Naughton, et al., Design considerations for an optical link supporting intersatellite quantum key distribution, Optical Engineering 58(1), 016106 (2019).
[4] R. Bedington, et al., Nanosatellite experiments to enable future space-based QKD missions, EPJ Quantum Technology 2016 3:12 (2016).

Autor: Dr hab. Jakub Mielczarek - pracownik naukowy w Instytucie Fizyki na Uniwersytecie Jagiellońskim. W latach 2016-2018 Prezes Zarządu spółki Space Garden, odpowiedzialnej m.in. za utworzenie Habitatu Lunares w Pile. Jest kierownikiem zespołu naukowego Quantum Cosmos Lab (quantumcosmos.org), w ramach którego prowadzone są badania teoretyczne na styku teorii grawitacji i mechaniki kwantowej. Jednym z obszarów aktywności zespołu jest rozwijanie teoretycznych podstaw kwantowej komunikacji satelitarnej.